作者简介： 侯澄钧，俄亥俄州立大学运筹学博士，目前在美国从事财产事故险(Property & Casualty)领域的保险产品开发，涉及数据分析，统计建模，产品算法优化等方面的工作。

目录： • 模型简介 • 线性回归 • Logistic回归 • Elstic Net理论简介 • 学习资料

模型简介

Kaggle网站（https://www.kaggle.com/）成立于2010年，是当下最流行的进行数据发掘和预测模型竞赛的在线平台。与Kaggle合作的公司可以在网站上提出一个问题或者目标，同时提供相关数据，来自世界各地的计算机科学家、统计学家和建模爱好者，将受领任务，通过比较模型的某些性能参数，角逐出优胜者。通过大量的比赛，一系列优秀的数据挖掘模型脱颖而出，受到广大建模者的认同，被普遍应用在各个领域。在保险行业中用于拟合广义线性模型的LASSO回归就是其中之一。

LASSO回归的特点是在拟合广义线性模型的同时进行变量筛选（variable selection）和复杂度调整（regularization）。因此，不论目标因变量（dependent/response varaible）是连续的（continuous），还是二元或者多元离散的（discrete），都可以用LASSO回归建模然后预测。这里的变量筛选是指不把所有的变量都放入模型中进行拟合，而是有选择的把变量放入模型从而得到更好的性能参数。复杂度调整是指通过一系列参数控制模型的复杂度，从而避免过度拟合（overfitting）。对于线性模型来说，复杂度与模型的变量数有直接关系，变量数越多，模型复杂度就越高。更多的变量在拟合时往往可以给出一个看似更好的模型，但是同时也面临过度拟合的危险。此时如果用全新的数据去验证模型（validation），通常效果很差。一般来说，变量数大于数据点数量很多，或者某一个离散变量有太多独特值时，都有可能过度拟合。

LASSO回归复杂度调整的程度由参数 λ 来控制，λ 越大对变量较多的线性模型的惩罚力度就越大，从而最终获得一个变量较少的模型。 LASSO回归与Ridge回归同属于一个被称为Elastic Net的广义线性模型家族。这一家族的模型除了相同作用的参数 λ 之外，还有另一个参数 α 来控制应对高相关性（highly correlated）数据时模型的性状。 LASSO回归 α=1，Ridge回归 α=0，一般Elastic Net模型 0<α<1。这篇文章主要介绍LASSO回归，所以我们集中关注 α=1 的情况，对于另外两种模型的特点和如何选取最优 α 值，我会在章节“Elstic Net模型家族简介”做一些简单阐述。

目前最好用的拟合广义线性模型的R package是 glmnet，由LASSO回归的发明人，斯坦福统计学家Trevor Hastie领衔开发。它的特点是对一系列不同 λ 值进行拟合，每次拟合都用到上一个 λ 值拟合的结果，从而大大提高了运算效率。此外它还包括了并行计算的功能，这样就能调动一台计算机的多个核或者多个计算机的运算网络，进一步缩短运算时间。

下面我们就通过一个线性回归和一个Logistic回归的例子，了解如何使用 glmnet 拟合LASSO回归。另外，之后的系列文章我打算重点介绍非参数模型（nonparametric model）中的一种，Gradient Boosting Machine。然后通过一个保险行业的实例，分享一些实际建模过程中的经验，包括如何选取和预处理数据，如何直观得分析自变量与因变量之间的关系，如何避免过度拟合，如何衡量和选取最终模型。

线性回归

我们从最简单的线性回归（Linear Regression）开始了解如何使用 glmnet 拟合LASSO回归模型，所以此时的连接函数（link function）就是恒等，或者说没有连接函数，而误差的函数分布是正态分布。

首先我们装载 glmnet package，然后读入试验用数据“LinearExample.RData”，下载链接：

library(glmnet)
load("LinearExample.RData")

之后在workspace里我们会得到一个100×20的矩阵 x 作为输入自变量，100×1的矩阵 y 作为目标因变量。矩阵 x 代表了我们有100个数据点，每个数据点有20个统计量（feature）。现在我们就可以用函数 glmnet() 建模了：

fit = glmnet(x, y, family="gaussian", nlambda=50, alpha=1)

好，建模完毕，至此结束本教程 🙂

觉得意犹未尽的朋友可以接着看下面的内容。

参数 family 规定了回归模型的类型：

family="gaussian" 适用于一维连续因变量（univariate）
family="mgaussian" 适用于多维连续因变量（multivariate）
family="poisson" 适用于非负次数因变量（count）
family="binomial" 适用于二元离散因变量（binary）
family="multinomial" 适用于多元离散因变量（category）

参数 nlambda=50 让算法自动挑选50个不同的 λ 值，拟合出50个系数不同的模型。alpha=1输入 α 值，1是它的默认值。值得注意的是，glmnet 只能接受数值矩阵作为模型输入，如果自变量中有离散变量的话，需要把这一列离散变量转化为几列只含有0和1的向量，这个过程叫做One Hot Encoding。通过下面这个小例子，我们可以了解One Hot Encoding的原理以及方法：

df=data.frame(Factor=factor(1:5), Character=c("a","a","b","b","c"),
              Logical=c(T,F,T,T,T), Numeric=c(2.1,2.3,2.5,4.1,1.1))
model.matrix(~., df)

##   (Intercept) Factor2 Factor3 Factor4 Factor5 Characterb Characterc
## 1           1       0       0       0       0          0          0
## 2           1       1       0       0       0          0          0
## 3           1       0       1       0       0          1          0
## 4           1       0       0       1       0          1          0
## 5           1       0       0       0       1          0          1
##   LogicalTRUE Numeric
## 1           1     2.1
## 2           0     2.3
## 3           1     2.5
## 4           1     4.1
## 5           1     1.1
## attr(,"assign")
## [1] 0 1 1 1 1 2 2 3 4
## attr(,"contrasts")
## attr(,"contrasts")$Factor
## [1] "contr.treatment"
## 
## attr(,"contrasts")$Character
## [1] "contr.treatment"
## 
## attr(,"contrasts")$Logical
## [1] "contr.treatment"

除此之外，如果我们想让模型的变量系数都在同一个数量级上，就需要在拟合前对数据的每一列进行标准化（standardize），即对每个列元素减去这一列的均值然后除以这一列的标准差。这一过程可以通过在 glmnet() 函数中添加参数 standardize=TRUE 来实现。

回到我们的拟合结果 fit。作为一个R对象，我们可以把它当作很多函数的输入。比如说，我们可以查看详细的拟合结果：

print(fit)

## Call:  glmnet(x = x, y = y, family = "gaussian", alpha = 1, nlambda = 50) 
## 
##       Df   %Dev   Lambda
##  [1,]  0 0.0000 1.631000
##  [2,]  2 0.1476 1.351000
##  [3,]  2 0.2859 1.120000
##  [4,]  4 0.3946 0.927900
##  [5,]  5 0.5198 0.768900
##  [6,]  6 0.6303 0.637100
##  [7,]  6 0.7085 0.528000
##  [8,]  7 0.7657 0.437500
##  [9,]  7 0.8081 0.362500
## [10,]  7 0.8373 0.300400
## [11,]  7 0.8572 0.248900
## [12,]  8 0.8721 0.206300
## [13,]  8 0.8833 0.170900
## [14,]  8 0.8909 0.141600
## [15,]  8 0.8962 0.117400
## [16,]  9 0.8999 0.097250
## [17,]  9 0.9027 0.080590
## [18,] 10 0.9046 0.066780
## [19,] 11 0.9065 0.055340
## [20,] 15 0.9081 0.045850
## [21,] 16 0.9095 0.038000
## [22,] 17 0.9105 0.031490
## [23,] 18 0.9113 0.026090
## [24,] 19 0.9119 0.021620
## [25,] 19 0.9123 0.017910
## [26,] 19 0.9126 0.014840
## [27,] 19 0.9128 0.012300
## [28,] 19 0.9129 0.010190
## [29,] 19 0.9130 0.008446
## [30,] 19 0.9131 0.006999
## [31,] 20 0.9131 0.005800
## [32,] 20 0.9131 0.004806
## [33,] 20 0.9132 0.003982
## [34,] 20 0.9132 0.003300
## [35,] 20 0.9132 0.002735
## [36,] 20 0.9132 0.002266

每一行代表了一个模型。列 Df 是自由度，代表了非零的线性模型拟合系数的个数。列 %Dev 代表了由模型解释的残差的比例，对于线性模型来说就是模型拟合的R^2（R-squred）。它在0和1之间，越接近1说明模型的表现越好，如果是0，说明模型的预测结果还不如直接把因变量的均值作为预测值来的有效。列 Lambda 当然就是每个模型对应的 λ 值。我们可以看到，随着 λ 的变小，越来越多的自变量被模型接纳进来，%Dev 也越来越大。第31行时，模型包含了所有20个自变量，%Dev 也在0.91以上。其实我们本应该得到50个不同的模型，但是连续几个 %Dev 变化很小时 glmnet() 会自动停止。分析模型输出我们可以看到当 Df 大于9的时候，%Dev 就达到了0.9，而且继续缩小 λ，即增加更多的自变量到模型中，也不能显著提高 %Dev。所以我们可以认为当 λ 接近0.1时，得到的包含9个自变量的模型，可以相当不错的描述这组数据。

我们也可以通过指定 λ 值，抓取出某一个模型的系数：

coef(fit, s=c(fit$lambda[16],0.1))

## 21 x 2 sparse Matrix of class "dgCMatrix"
##                        1            2
## (Intercept)  0.150672014  0.150910983
## V1           1.322088892  1.320532088
## V2           .            .          
## V3           0.677692624  0.674955779
## V4           .            .          
## V5          -0.819674385 -0.817314761
## V6           0.523912698  0.521565712
## V7           0.007293509  0.006297101
## V8           0.321450451  0.319344250
## V9           .            .          
## V10          .            .          
## V11          0.145727982  0.142574921
## V12          .            .          
## V13          .            .          
## V14         -1.061733786 -1.060031309
## V15          .            .          
## V16          .            .          
## V17          .            .          
## V18          .            .          
## V19          .            .          
## V20         -1.025371209 -1.021771038

需要注意的是，我们把指定的 λ 值放在 s= 里，因为在后面Logistic回归的部分我们还用到了 s="lambda.min" 的方法指定 λ 的值。当指定的 λ 值不在 fit$lambda 中时，对应的模型系数由linear interpolation近似得到。我们还可以做图观察这50个模型的系数是如何变化的：

plot(fit, xvar="lambda", label=TRUE)

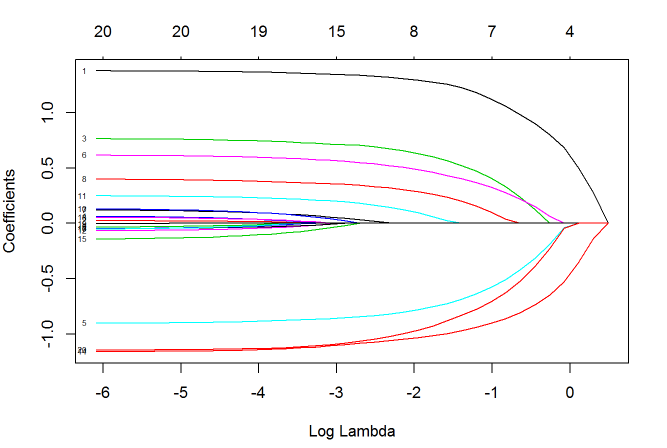
图中的每一条曲线代表了每一个自变量系数的变化轨迹，纵坐标是系数的值，下横坐标是 log⁡(λ)，上横坐标是此时模型中非零系数的个数。我们可以看到，黑线代表的自变量1在 λ 值很大时就有非零的系数，然后随着 λ 值变小不断变大。我们还可以尝试用 xvar="norm" 和 xvar="dev" 切换下横坐标。

接下来当然就是指定 λ 值，然后对新数据进行预测了：

set.seed(91)
nx = matrix(rnorm(5*20),5,20)
predict(fit, newx=nx, s=c(fit$lambda[16],0.1))

##               1          2
## [1,]  2.0309573  2.0273151
## [2,] -1.9362780 -1.9328610
## [3,]  1.1048789  1.1047725
## [4,]  0.5156294  0.5154747
## [5,]  1.4621024  1.4618535

下面我们再来看几个 glmnet() 函数的其他功能。使用 upper.limits 和 lower.limits，我们可以指定模型系数的上限与下限：

lfit=glmnet(x, y, lower=-.7, upper=.5)
plot(lfit, xvar="lambda", label=TRUE)

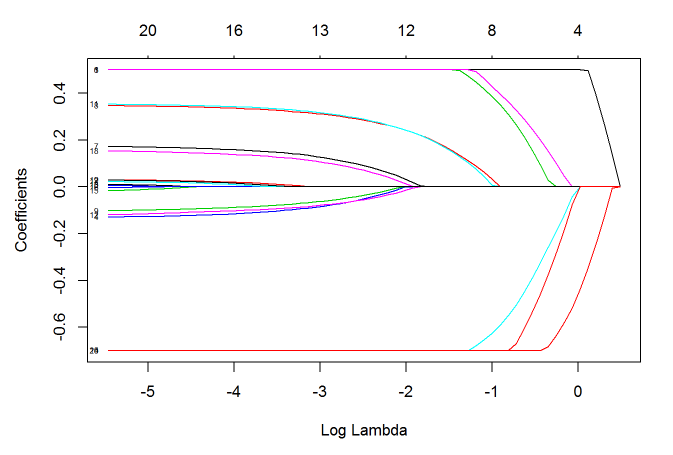
上限与下限可以是一个值，也可以是一个向量，向量的每一个值作为对应自变量的参数上下限。有时，在建模之前我们就想凸显某几个自变量的作用，此时我们可以调整惩罚参数。每个自变量的默认惩罚参数是1，把其中的某几个量设为0将使得相应的自变量不遭受任何惩罚：

p.fac = rep(1, 20)
p.fac[c(5, 10, 15)] = 0
pfit = glmnet(x, y, penalty.factor=p.fac)
plot(pfit, xvar="lambda", label = TRUE)

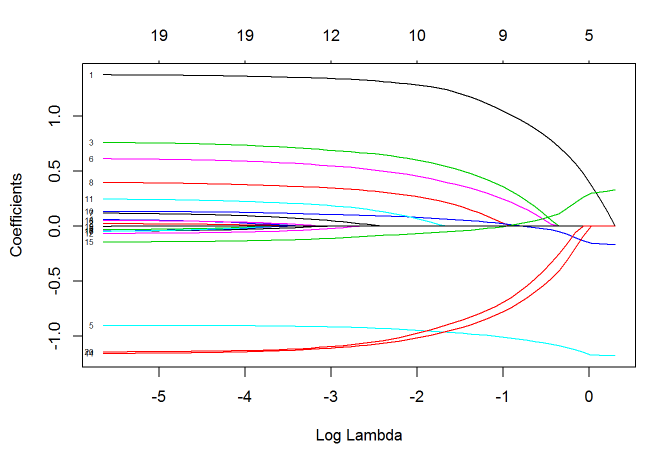
我们可以看到，自变量5/10/15的系数一直不为0，而其他的参数系数绝对值随着 λ 值变小而变大。

Logistic回归

当面对离散因变量时，特别是面对二元因变量（Yes/No）这样的问题时，Logistic回归被广泛使用。此时我们用 family="binomial" 来应对这种目标因变量是二项分布（binomial）的情况。

试验用数据“LogisticExample.RData”里储存了100×30的矩阵 x，和元素是0/1长度是100的向量 y，下载链接：

load("LogisticExample.RData")

我们可以用上一节介绍的 glmnet() 函数来拟合模型，然后选取最优的 λ 值。但是在这种方法下，所有数据都被用来做了一次拟合，这很有可能会造成过拟合的。此时，当我们把得到的模型用来预测全新收集到的数据时，结果很可能会不尽如人意。所以只要条件允许，我们都会用交叉验证（cross validation）拟合进而选取模型，同时对模型的性能有一个更准确的估计。

set.seed(91)
cvfit = cv.glmnet(x, y, family = "binomial", type.measure = "class")

这里的 type.measure 是用来指定交叉验证选取模型时希望最小化的目标参量，对于Logistic回归有以下几种选择：

type.measure="deviance" 使用deviance，即-2倍的log-likelihood
type.measure="mse" 使用拟合因变量与实际应变量的mean squred error
type.measure="mae" 使用mean absolute error
type.measure="class" 使用模型分类的错误率（missclassification error）
type.measure="auc" 使用area under ROC curve，是现在最流行的综合考量模型性能的一种参数

除此之外，在 cv.glmnet() 里我们还可以用 nfolds 指定fold数，或者用 foldid 指定每个fold的内容。因为每个fold间的计算是独立的，我们还可以考虑运用并行计算来提高运算效率，使用 parallel=TRUE 可以开启这个功能。但是我们需要先装载package doParallel。下面我们给出在Windows操作系统和Linux操作系统下开启并行

library(doParallel)
# Windows System
cl &lt;- makeCluster(6)
registerDoParallel(cl)
cvfit = cv.glmnet(x, y, family = "binomial", type.measure = "class", parallel=TRUE)
stopCluster(cl)
# Linux System
registerDoParallel(cores=8)
cvfit = cv.glmnet(x, y, family = "binomial", type.measure = "class", parallel=TRUE)
stopImplicitCluster()

同样的，我们可以绘制 cvfit 对象：

plot(cvfit)

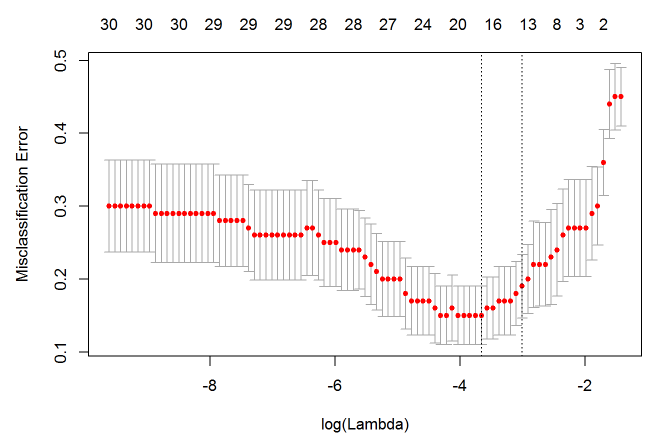
因为交叉验证，对于每一个 λ 值，在红点所示目标参量的均值左右，我们可以得到一个目标参量的置信区间。两条虚线分别指示了两个特殊的 λ 值：

c(cvfit$lambda.min, cvfit$lambda.1se)

## [1] 0.03741031 0.05956780

lambda.min 是指在所有的 λ 值中，得到最小目标参量均值的那一个。而 lambda.1se 是指在 lambda.min 一个方差范围内得到最简单模型的那一个 λ 值。因为 λ 值到达一定大小之后，继续增加模型自变量个数即缩小 λ 值，并不能很显著的提高模型性能， lambda.1se 给出的就是一个具备优良性能但是自变量个数最少的模型。同样的，我们可以指定 λ 值然后进行预测：

predict(cvfit, newx=x[1:5,], type="response", s="lambda.1se")

##              1
## [1,] 0.2992175
## [2,] 0.8319748
## [3,] 0.6160852
## [4,] 0.2180918
## [5,] 0.6416046

这里的 type 有以下几种选择：

type="link" 给出线性预测值，即进行Logit变换之前的值
type="response" 给出概率预测值，即进行Logit变换之后的值
type="class" 给出0/1预测值
type="coefficients" 罗列出给定 λ 值时的模型系数
type="nonzero" 罗列出给定 λ 值时，不为零模型系数的下标

另外，当已有了一个模型之后，我们又得到了几个新的自变量，如果想知道这些新变量能否在第一个模型的基础上提高模型性能，可以把第一个模型的预测因变量作为一个向量放到函数选项 offset 中，再用 glmnet 或者 cv.glmnet 进行拟合。

Elstic Net模型家族理论简介

在这一节我们会了解一些关于Elastic Net模型家族的理论。首先我们先来看看一般线性Elastic Net模型的目标函数：

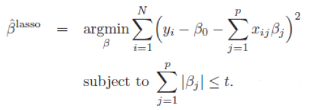
目标函数的第一行与传统线性回归模型完全相同，即我们希望得到相应的自变量系数 $\beta$，以此最小化实际因变量y与预测应变量 $\beta x$ 之间的误差平方和。而线性Elastic Net与线性回归的不同之处就在于有无第二行的这个约束，线性Elastic Net希望得到的自变量系数是在由 $t$ 控制的一个范围内。这一约束也是Elastic Net模型能进行复杂度调整，LASSO回归能进行变量筛选和复杂度调整的原因。我们可以通过下面的这张图来解释这个道理：

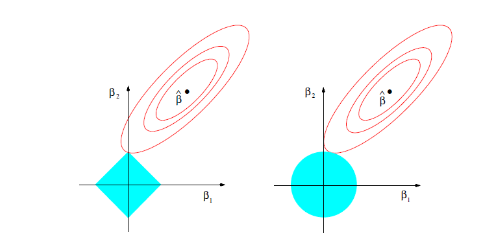
先看左图，假设一个二维模型对应的系数是 $\beta_1$ 和 $\beta_2$，然后 $\hat{\beta}$ 是最小化误差平方和的点，即用传统线性回归得到的自变量系数。但我们想让这个系数点必须落在蓝色的正方形内，所以就有了一系列围绕 $\hat{\beta}$ 的同心椭圆，其中最先与蓝色正方形接触的点，就是符合约束同时最小化误差平方和的点。这个点就是同一个问题LASSO回归得到的自变量系数。因为约束是一个正方形，所以除非相切，正方形与同心椭圆的接触点往往在正方形顶点上。而顶点又落在坐标轴上，这就意味着符合约束的自变量系数有一个值是0。所以这里传统线性回归得到的是 $\beta_1$ 和 $\beta_2$ 都起作用的模型，而LASSO回归得到的是只有 $\beta_2$ 有作用的模型，这就是LASSO回归能筛选变量的原因。

而正方形的大小就决定了复杂度调整的程度。假设这个正方形极小，近似于一个点，那么LASSO回归得到的就是一个只有常量（intercept）而其他自变量系数都为0的模型，这是模型简化的极端情况。由此我们可以明白，控制复杂度调整程度的 λ 值与约束大小 $t$ 是呈反比的，即 λ 值越大对参数较多的线性模型的惩罚力度就越大，越容易得到一个简单的模型。

另外，我们之前提到的参数 α 就决定了这个约束的形状。刚才提到LASSO回归（α=1）的约束是一个正方形，所以更容易让约束后的系数点落在顶点上，从而起到变量筛选或者说降维的目的。而Ridge回归（α=0）的约束是一个圆，与同心椭圆的相切点会在圆上的任何位置，所以Ridge回归并没有变量筛选的功能。相应的，当几个自变量高度相关时，LASSO回归会倾向于选出其中的任意一个加入到筛选后的模型中，而Ridge回归则会把这一组自变量都挑选出来。至于一般的Elastic Net模型（0<α<1），其约束的形状介于正方形与圆形之间，所以其特点就是在任意选出一个自变量或者一组自变量之间权衡。

下面我们就通过Logistic回归一节的例子，来看看这几种模型会得到怎样不同的结果：

# CV for 11 alpha value
for (i in 0:10) {
  assign(paste("cvfit", i, sep=""),
  cv.glmnet(x, y, family="binomial", type.measure="class", alpha=i/10))
}
# Plot Solution Paths
par(mfrow=c(3,1))
plot(cvfit10, main="LASSO")
plot(cvfit0, main="Ridge")
plot(cvfit5, main="Elastic Net")

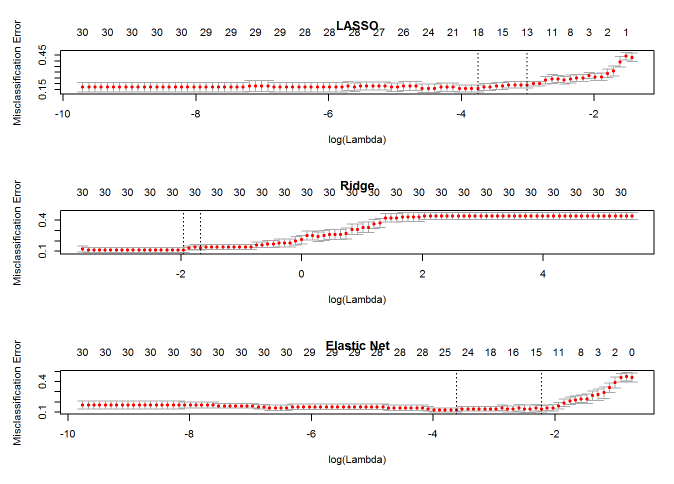
通过比较可以看出，Ridge回归得到的模型一直都有30个自变量，而 α=0.5 时的Elastic Net与LASSO回归有相似的性能。

学习资料

本文的图片来自Trevor Hastie教授的著作“The Elements of Statistical Learning”，我觉得这本书在parametric model这一方向的阐述尤其精彩，对于其他数据挖掘方向也有十分全面的介绍。

更全面关于glmnet的应用，可以参考 https://web.stanford.edu/~hastie/glmnet/glmnet_alpha.html，本文的两个例子也出自这篇vignette。

关于Elastic Net模型家族的特点和优劣，可以参考 http://www4.stat.ncsu.edu/~post/josh/LASSO_Ridge_Elastic_Net_-_Examples.html。

最后，感谢COS编辑部的指正，也感谢大家的阅读。

热门数据挖掘模型应用入门（一）: LASSO回归

侯澄钧

模型简介

线性回归

Logistic回归

Elstic Net模型家族理论简介

学习资料

关于作者

侯澄钧